Binary Search Tree

Introduction

Prerequisites: Set, Binary Tree

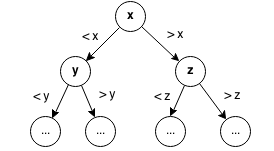
A binary search tree is a binary tree with special properties. For every node in the tree, the values of all the nodes in left subtree of a node will always be less than the value of the node and all the nodes in the right subtree will always be more than the value of the node. It has a recursive structure meaning every subtree is also a binary search tree.

Structure:

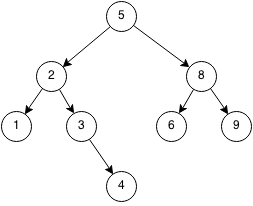
Example:

Class

In a binary search tree, everything to the left of a node is smaller than that node and everything to the right of that node is greater than that node.

Structure:

Example:

Implementation

A Node is a node in our binary search tree. Each node will contain a left subtree, a right subtree, the parent of the tree and the value stored at that node. It is unnecessary to store the parent, but for this implementation it will be easier to keep track of the parent.

replaceChild replaces the left or right child node specified with the replacement node.

public class Node {
  int value;
  Node left;
  Node right;
  Node parent;

  public Node(int val, Node parent) {
    this.value = val;
    this.left = null;
    this.right = null;
    this.parent = parent;
  }

  // Replaces the child node with the replacement one.
  public void replaceChild(Node child, Node replacement) {
    // If replacing left child.
    if (left == child) {
      left = replacement;
    }
    // If replacing right child.
    if (right == child) {
      right = replacement;
    }
    // Set replacement nodes parent.
    if (replacement != null) {
      replacement.parent = this;
    }
  }
}

In our class we will store the number of element in the set and the root of the tree. From the root of the tree we can traverse the rest of the tree.

public class BinarySearchTree {
  int size;
  Node root;
    
  public BinarySearchTree(){
    size = 0;
    root = null;
  }
}

Insert

To insert an element in the tree set we search for the element that we are trying to insert. If it is already there then the operation fails because sets contain unique elements. Otherwise we will insert the new element into the set.

Let's insert 4 into the binary search tree. We first start at the root at 5.

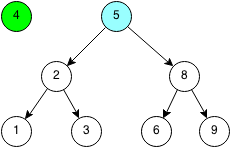
Since 4 is less than 5, we traverse the left subtree to 2.

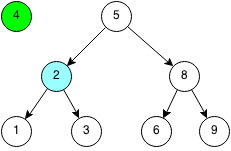
Since 4 is greater than 2, we traverse the right subtree to 3.

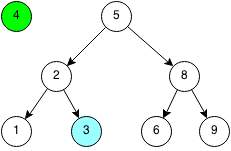
Since 4 is greater than 3 and there is no right child, than we create a new node with the value 4 as the right child.

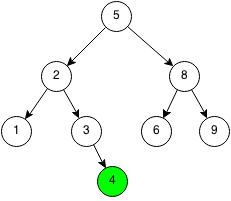
Implementation

public boolean insert(int x) {
  // If root is missing.
  if (root == null) {
    root = new Node(x, null);
    size = 1;
    return true;
  }
  Node curTree = root;
  while (curTree != null) {
    // Return if x already exists in set.
    if (x == curTree.value) {
      return false;
    }
    // Traverse left if x is less than current node.
    else if (x < curTree.value) {
      // If left child is empty, create new node.
      if (curTree.left == null) {
        curTree.left = new Node(x, curTree);
        size++;
        return true;
      }
      // Traverse left child.
      curTree = curTree.left;
    }
    // Traverse right otherwise.
    else {
      // If right child is empty, create new node.
      if (curTree.right == null) {
        curTree.right = new Node(x, curTree);
        size++;
        return true;
      }
      // Traverse right child.
      curTree = curTree.right;
    }
  }
  return false;
}

Contains

To check if the tree set contains an element, we search for it in the binary tree by starting at the root. If the number is less than the current, we search the left subtree. If the number is greater than the current, we search the right subtree.

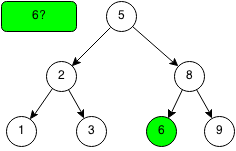
We want to check if the number 6 is in the binary search tree.

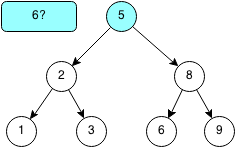
Since 6 is larger than 5, we traverse the right subtree of 5.

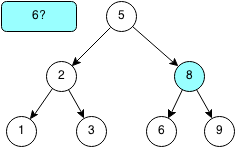
Since 6 is less than 8, we traverse the left subtree of 8.

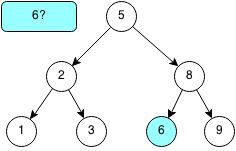
The root of the left subtree is 6, thus we have found the element. If we were to keep traversing and reach a leaf node that was not the element, then the element would not exist in the binary search tree.

Implementation

public boolean contains(int x) {
  Node curTree = root;
  // Iterate through tree.
  while (curTree != null) {
    // If found element return true.
    if (x == curTree.value) {
      return true;
    }
    // Traverse left tree if x is less than current node.
    else if (x < curTree.value) {
      curTree = curTree.left;
    }
    // Traverse right tree if x is greater then current node.
    else {
      curTree = curTree.right;
    }
  }
  // Return false if not found.
  return false;
}

Remove

Removing an element is a much more complex because we need to maintain the tree structure of the tree set when removing elements. First, we locate the element that we want to remove. If the element is not there, then the operation failed and we return false. If the element is there, then are three cases we need to consider.

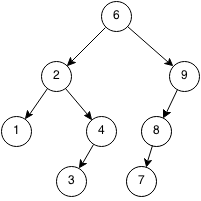
Case 1: Node is a leaf node

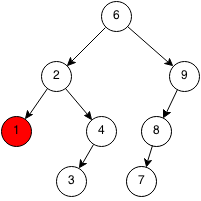
If the node we want to remove is the leaf node, we can simply remove it.

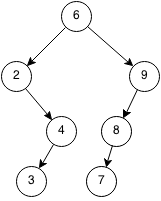
Case 2: Node has one child

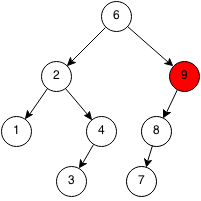
If the node we want to remove has a child, we can replace that node with its' only child.

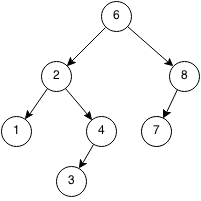
Case 3: Node has two children

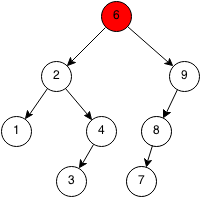
We need to replace the node with the rightmost of the left subtree or the leftmost of the right subtree to maintain the order.

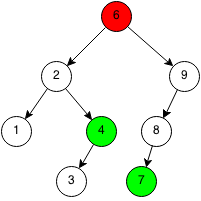
It does not matter which side we pick, so we will use the rightmost of the left subtree. First, we copy the value of the rightmost of the left subtree into the node that will be deleted.

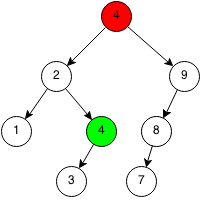
Then we replace the rightmost of the left subtree with its left subtree.

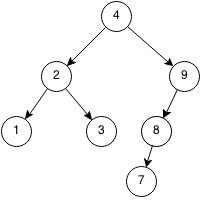
Implementation

public boolean remove(int x) {
  // Node to be removed.
  Node curNode = root;

  // Traverse through binary tree.
  while (curNode != null) {
    // If found element, use node.
    if (x == curNode.value) {
      break;
    }
    // Traverse through left child.
    else if (x < curNode.value) {
      curNode = curNode.left;
    }
    // Traverse through right child.
    else {
      curNode = curNode.right;
    }
  }
  // If node was not found, return false.
  if (curNode == null) {
    return false;
  }
  // Case 1: Removed node has no children.
  if (curNode.left == null && curNode.right == null) {
    // Special case if root.
    if (curNode == root) {
      this.root = null;
    }
    // Replace node with null.
    else {
      curNode.parent.replaceChild(curNode, null);
    }
  }
  // Case 2a: Removed node only has a right child.
  else if (curNode.left == null) {
    // Special case if node is root.
    if (curNode == root) {
      root = curNode.right;
      root.parent = null;
    }
    // Replace current node with right child.
    else {
      curNode.parent.replaceChild(curNode, curNode.right);
    }
  }
  // Case 2b: Removed node only has a left child.
  else if (curNode.right == null) {
    // Special case if node is root.
    if (curNode == root) {
      root = curNode.left;
      root.parent = null;
    }
    // Replace current node with left child.
    else {
      curNode.parent.replaceChild(curNode, curNode.left);
    }
  }
  // Case 3: Removed node has two children.
  else {
    // Get rightmost of left subtree.
    Node rightmost = curNode.left;
    while (rightmost.right != null) {
      rightmost = rightmost.right;
    }
    // Copy rightmost of left subtree to removed node's.
    curNode.value = rightmost.value;
    // Replace rightmost of left subtree with left child.
    rightmost.parent.replaceChild(rightmost, rightmost.left);
  }
  size--;
  return true;
}

Print Tree

In a binary search tree, we can print the elements in order.

Implementation

public String dfs(Node curTree) {
  if (curTree == null) {
    return "";
  }
  String ret = "";
  // Print left child.
  ret += dfs(curTree.left);
  // Print current node.
  ret += curTree.value;
  ret += ",";
  // Print right child.
  ret += dfs(curTree.right);
  return ret;
}
    
public String toString() {
  String ret = "";
  if (root != null) {
    ret += dfs(root);
  }
  return ret.substring(0, ret.length() - 1);
}

Exercises

1. Write a function to determine if a binary tree is a binary search tree.