Introduction
A connected component is a subgraph where all the vertices in the subgraph connect to each other.
Finding the number of distinct connected components can be done using a breadth first search or a depth first search.
Finding the number the connected components for each node can be done with a simple algorithm.
Implementation
- Set each node's parent to itself.
- Pick an unused edge in the graph that is from node A to node B, if the parent of A is not the same as parent of B then set all nodes whose parent is B to parents of A.
- Repeat for all edges.
Example
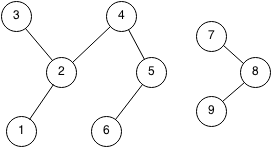
We select a random edge from node 1 and node 2. We set the parent node of 2 to node 1.
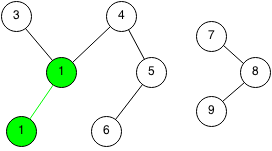
We select another random edge from node 5 to node 6.
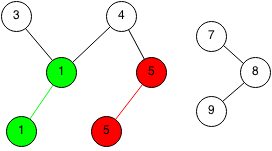
We pick another random edge and we set the parent to 5.
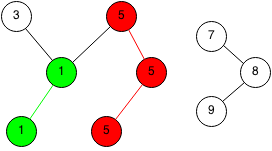
We take another random edge and we set the parents to 7.
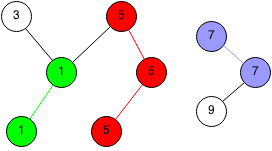
We take another random edge and we have an interesting case, two connected components are to be connected. We take all the nodes whose parent is 1, and we set the new parent to 5.
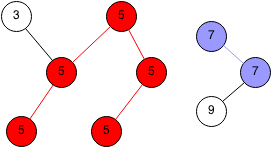
We take another random edge and set its parent to 1.
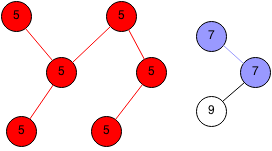
We take the last edge and set the last node parent to 7.
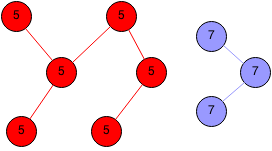
Java Code
public static int getParent(int x, int[] parent) {
// If nodes parent is itself, then we reach the highest parent.
if (parent[x] == x) {
return x;
}
// Set current node's parent to highest parent.
parent[x] = getParent(parent[x], parent);
// Return highest parent.
return parent[x];
}
public static void connectedComponents(int adjMatrix[][]) {
int n = adjMatrix.length;
int[] parent = new int[n];
int i, j;
// Initialize every nodes parent to itself.
for (i = 0; i < n; i++) {
parent[i] = i;
}
// Iterate through each node.
for (i = 0; i < n; i++) {
// Iterate through each other node.
for (j = 0; j < n; j++) {
// If the two nodes have an edge.
if (adjMatrix[i][j] > 0) {
// Recursively get root parents of each node.
int pi = getParent(i, parent);
int pj = getParent(j, parent);
// Set parent of one to the other if they are different.
if (pi != pj) {
parent[pj] = pi;
}
}
}
}
}