Introduction
Prerequisites: Shortest Path, Dynamic Programming
Floyd Warshall is a algorithm for finding the shortest distances between all pairs of nodes in a graph. The algorithm has a runtime of O(n3) and is able to detect cycles.
Implementation
Floyd-Warshall uses a dynamic programming approach to finding the shortest path between node A and node B. Every path from node A to node B can be rewritten as a path from A to some node in between plus the path from the node in between to node B. The shortest path from A to B can be found by finding a node C such that the shortest path from A to C plus the shortest path from C to B is minimized.
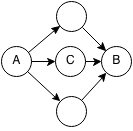
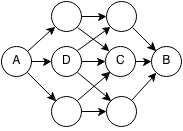
Formalization
Here is a recursive definition of the Floyd-Warshall algorithm:
Given a directed graph with N nodes and edges between nodes:
Let edge(i,j) be the weight of the edge from node i to node j in the graph
Let shortestPath(i,j) be the shortest path from i to j
Base Case:
shortestPath(i,i) = 0
Recursion:
shortestPath(i,j) = minimum of:
minimum of (shortestPath(i,k) + shortestPath(k,j) for all unvisited nodes k)
edge(i,j) if exists
Code
class edge {
int weight, source, dest;
public edge(int source, int dest, int weight) {
this.source = source;
this.dest = dest;
this.weight = weight;
}
}
public static final int UNDEFINED = Integer.MIN_VALUE;
public static int[][] FloydWarshall(Vector<Vector<edge>> adjList) {
int n = adjList.size();
// Let dist[i][j] be the minimum distance from i to j.
int[][] dist = new int[n][n];
// Initialize all minimum distances to be undefined.
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[i][j] = UNDEFINED;
}
}
// The minimum distance from a node to itself is 0.
for (int i = 0; i < n; i++) {
dist[i][i] = 0;
}
// Set distances for each edge.
for (int i = 0; i < n; i++) {
for (int j = 0; j < adjList.get(i).size(); j++) {
edge e = adjList.get(i).get(j);
dist[e.source][e.dest] = e.weight;
}
}
// Iterate through each intermediate node.
for (int k = 0; k < n; k++) {
// Iterate through each starting node.
for (int i = 0; i < n; i++) {
// Iterate through each ending node.
for (int j = 0; j < n; j++) {
// If there is a path from i to k and k to j.
if (dist[i][k] != UNDEFINED && dist[k][j] != UNDEFINED) {
// Distance from i to j is distance from i to k plus distance from k
// to j.
int newDist = dist[i][k] + dist[k][j];
// Update distance from i to j, if the new distance is less than
// current distance or if there is no existing path from i to j.
if (dist[i][j] > newDist || dist[i][j] == UNDEFINED) {
dist[i][j] = newDist;
}
}
}
}
}
// Check if there are negative cycles.
for (int i = 0; i < n; i++) {
// If the distance from a node to itself is negative, then there is a
// negative cycle.
if (dist[i][i] < 0) {
System.out.println("negative cycle");
}
}
return dist;
}
Exercises
- Prove Floyd Warshall works.
- Extend Floyd Warshall to return the order of nodes in a shortest path from the start to end (e.g. A→B→C)..