Prim's

Introduction

Prerequisites: Priority Queue, Minimum Spanning Tree

Prim's algorithm is a greedy algorithm that finds the minimum spanning tree in a graph.

If implemented efficiently using a priority queue, the runtime is O(n log n).

Implementation

Prim's algorithm finds the minimum spanning tree using a greedy fashion. It works as such:

1. Pick an arbitrary node.
2. Find the closest node to that node.
3. Find the closest node to the 2 nodes.
4. Find the closest node to the 3 nodes.
5. ...
6. Find the closest node to n-1 nodes.

The closest node is the node with the lowest cost edge to the already connected nodes.

Example

Suppose we have the following graph and we would like the find the minimum spanning tree.

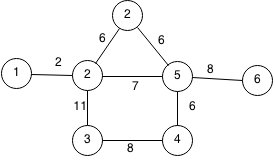
We can start at any random node so this example, we will start at 1.

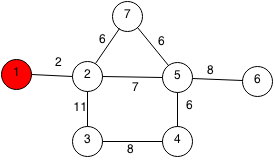
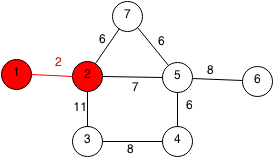
The closest unpicked node to all the chosen nodes is 2 at a cost of 2.

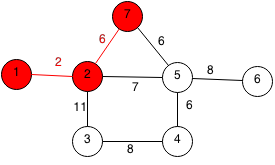
The closest unpicked node to all the chosen nodes is 7 at a cost of 6.

The closest unpicked node to all the chosen nodes is 5 at a cost of 6.

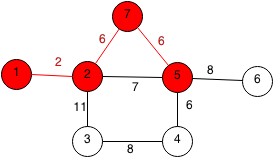
The closest unpicked node to all the chosen nodes is 4 at a cost of 6.

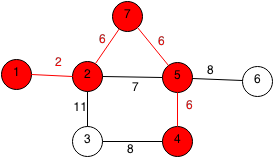
The closest unpicked node to all the chosen nodes is 6 at a cost of 8.

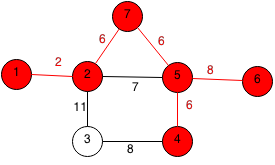
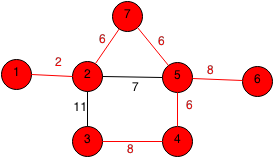
The last node to be chosen is 3 with a cost of 8.

Java Code

We can implement Prim's algorithm in Java efficiently with a priority queue of edges using the weight as the comparing property.

class node implements Comparable<node> {
  int weight, index;
  public node(int weight, int index) {
    this.weight = weight;
    this.index = index;
  }
  public int compareTo(node e) {
    return weight - e.weight;
  }
}
public static int Prims(Vector<Vector<node>> adjList) {
  // Current cost of MST.
  int cost = 0;
  int n = adjList.size();
  
  PriorityQueue<node> pq = new PriorityQueue<node>();
  
  // Keep track if each node is visited.
  boolean visited[] = new boolean[n];
  for (int i = 0; i < n; i++) {
    visited[i] = false;
  }
  
  // Number of nodes visited.
  int inTree = 1;
  
  // Mark starting node as visited.
  visited[0] = true;
  
  // Add all edges of starting node.
  for (int i = 0; i < adjList.get(0).size(); i++) {
    pq.add(adjList.get(0).get(i));
  }
  // Keep going until all nodes visited.
  while (!pq.isEmpty() && inTree < n) {
    // Get the edge with the smallest weight.
    node cur = pq.poll();
    // Skip if node already used.
    if (visited[cur.index]) {
      continue;
    }
    inTree++;
    visited[cur.index] = true;
    cost += cur.weight;
    // Add all the edges of the new node to the priority queue.
    for (int i = 0; i < adjList.get(cur.index).size(); i++) {
      pq.add(adjList.get(cur.index).get(i));
    }
  }
  // Graph not connected if number of nodes used is less than total nodes.
  if (inTree < n) {
    return -1;
  }

  return cost;
}

Exercises

1. Prove that Prim's algorithm works.
2. Extends Prim's to output all the edges used.