Introduction
Quick Sort is another fast sorting algorithm that uses divide and conquer. In quick sort, an element is selected as a "pivot". The list is then divided into two sublists: a list of elements less than (or equal to) the pivot and a list of elements greater than the pivot. Each sublist is sorted and then appended together along with the origin pivot.
Implementation
Formalization
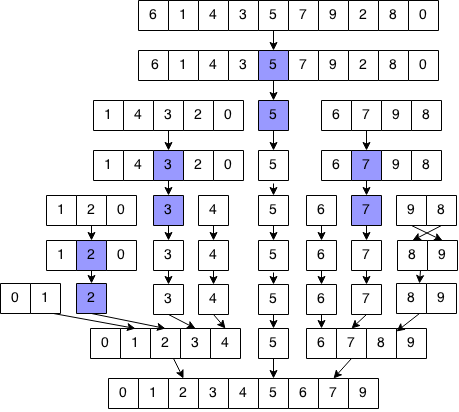
Let quicksort(array) sort the array using quicksort Base case: quicksort([]) = [] quicksort([x]) = [x] Recurrence: Let pivot be a random element in array quicksort(arr) = quicksort(arr[elements < pivot]) + [pivot] + quicksort(arr[elements >= pivot]) Example: quicksort([6,1,4,3,5,7,9,2,8,0]) = quicksort([1,4,3,2,0] + [5] + quicksort([6,7,9,8]) = (quicksort([1,2,0]) + [3] + quicksort([4])) + [5] + (quicksort([6]) + [7] + quicksort([9,8])) = (quicksort([0,1]) + [2] + quicksort([]) + [3] + [4]) + [5] + ([6] + [7] + [8, 9]) = (([0, 1] + [2] + []) + [3] + [4]) + [5] + ([6] + [7] + [8, 9]) = [0, 1, 2, 3, 4] + [5] + [6, 7, 8, 9] = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Code
We will implement our solution in Java that reflects our formalization in a way that is easier to understand, but more inefficient. In our code, we create new arrays to store partitions and merged results but we can actually do this in place without extra memory (left as an exercise).
// Quick sorts array from [first..last]
public static Vector<Integer> quickSort(Vector<Integer> arr) {
// Base case if sorting one or zero elements.
if (arr.size() <= 1) {
return arr;
}
// Select a random pivot.
int pivot = (int) (Math.random() * arr.size());
// Store each part.
Vector<Integer> lower = new Vector<Integer>();
Vector<Integer> higher = new Vector<Integer>();
Vector<Integer> equal = new Vector<Integer>();
// Splits element into each part.
for (int i = 0; i < arr.size(); i++) {
if (arr.get(i) < arr.get(pivot)) {
lower.add(arr.get(i));
}
else if (arr.get(i) > arr.get(pivot)) {
higher.add(arr.get(i));
}
else {
equal.add(arr.get(i));
}
}
// Combine results of all parts.
Vector<Integer> result = new Vector<Integer>();
result.addAll(quickSort(lower));
result.addAll(quickSort(equal));
result.addAll(quickSort(higher));
return result;
}
Exercises
- Rewrite quickSort such that we do not use any additional memory (i.e. rearranging into parts is done in place in the array and we do not create any additional vector or arrays). You should rewrite the function to sort in place: void quickSort(int arr[], int start, int end).