Introduction
An adjacency matrix stores a graph of N nodes with a two dimensional NxN array. We let adjMatrix[i][j] represents the weight between the node i and node j. If we have a sparse graph which has many nodes but few edges, the memory storage will be very inefficient and it would be better to use an adjacency list. However, if the graph is very dense, or there are few nodes, then an adjacency matrix is quick and easy to use. Checking if an edge exists between two nodes is O(1).
Example:
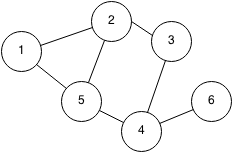
The adjacency matrix of the graph is:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 | 1 |
| 5 | 1 | 1 | 0 | 1 | 0 | 0 |
| 6 | 0 | 0 | 0 | 1 | 0 | 0 |
Implementation
class edge {
int weight, source, dest;
public edge(int source, int dest, int weight) {
this.source = source;
this.dest = dest;
this.weight = weight;
}
}
public static int[][] getAdjMatrix(Vector<edge> edges, int n) {
int adjMatrix[][] = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
adjMatrix[i][j] = 0;
}
}
for (int i = 0; i < edges.size(); i++) {
edge e = edges.get(i);
adjMatrix[e.source][e.dest] = e.weight;
adjMatrix[e.dest][e.source] = e.weight;
}
return adjMatrix;
}