Cycle detection

Introduction

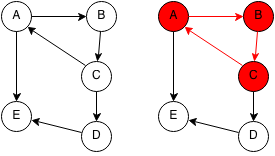
A cycle occurs in a graph when a duplicate node is encountered when traversing a tree using a depth first search. In other words, a cycle occurs when you can reach the same node through a path in a graph.

An undirected graph where the number of edges is greater than or equal to the number of nodes will always have cycles.

Implementation

We first mark every node as unvisited. We start at each unvisited node and we do a depth first search from that node. We mark each node along the way as temporarily visited and if we encounter a temporarily visited node, then we have a cycle. After temporarily visiting the nodes, we mark them as visited. If we reach a visited node again, then we stop since we already checked if that node had a cycle.

public static boolean hasCycle(int[][] adjMatrix) {
  int[] visited = new int[adjMatrix.length];
  
  // Mark each node as unvisited.
  for (int i = 0; i < adjMatrix.length; i++) {
    visited[i] = 0;
  }
  // Check if current node leads to a cycle.
  for (int i = 0; i < adjMatrix.length; i++) {
    if (hasCycleAt(adjMatrix, i, visited)) {
      return true;
    }
  }
  return false;
}

public static boolean hasCycleAt(int[][] adjMatrix, int i, int visited[]) {
  // If node has been reached again from the starting node, we have a cycle.
  if (visited[i] == 1) {
    return true;
  }
  // If node has been permanently visited, we know it was already checked.
  if(visited[i] == 2) {
    return false;
  }
  
  // Mark node as temporarily visited.
  visited[i] = 1;
  
  // Iterate through neighbors of current node.
  for (int j = 0; j < adjMatrix.length; i++) {
    if (adjMatrix[i][j] > 0) {
      // Recursively check is 
      if (hasCycleAt(adjMatrix, j, visited)) {
        return true;
      }
      visited[j] = 0;
    }
  }
  // Permanently mark node as visited.
  visited[i] = 2;
  return false;
}