Introduction
Prerequisites: Sets, Linked List
Hash sets are sets that use hashes to store elements. A hashing algorithm is an algorithm that takes an element and converts it to a chunk of a fixed size called a hash. For example, let our hashing algorithm be (x mod 10). So the hashes of 232, 217 and 19 are 2,7, and 9 respectively.
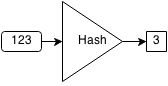
For every element in a hash set, the hash is computed and elements with the same hash are grouped together. This group of similar hashes is called a bucket and they are usually stored as linked lists.
If we want to check if an element already exists within the set, we first compute the hash of the element and then search through the bucket associated with the hash to see if the element is contained.
| Operation | Membership | Insertion | Deletion |
|---|---|---|---|
| Time Complexity | O(1) | O(1) | O(1) |
Class
Inside our implementation of a hash set, we will store the buckets (using an array of linked lists), the number of buckets, and the number of elements in the set.
The collision chance is the threshold for resizing the hash set. When the ratio of elements in the set to number of buckets is greater than the threshold, then the chance of collision will be high enough that it will slow down the operations. The lower this ratio, the better performing a hash set will be.
public class HashSet {
public LinkedList<Integer>[] buckets;
public int bucketsSize = 10;
public int size = 0;
public static final double COLLISION_CHANCE = 0.3;
public HashSet() {
// Create buckets.
buckets = new LinkedList[10];
for (int i = 0; i < bucketsSize; i++) {
buckets[i] = new LinkedList<Integer>();
}
size = 0;
}
}
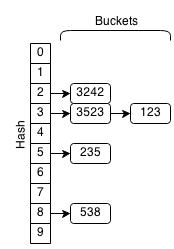
If we wanted to check if 7238 was in the hash set, we would get the hash (7238 mod 10 = 8). So we get the bucket associated with the hash 8 and we get the list of [538]. When we iterate through this short list, we see that 7238 is not a member of the set.
Similarly, if we wanted to insert 7238 into the hash set, we would check if it exists and if it did not, we would add the element to the bucket. For deletion, we would find 7238 and then remove it from the bucket if it existed.
Hash sets are very efficient in all three set operations if a good hashing algorithm is used. When the objects are that being stored are large then hash sets are effective as a set.
Hash code
The hash code is the result of the hashing algorithm for an element. In our hash set implementation, we will use a simple hash: modulus of the integer by the number of buckets.

For the most part, if the numbers are all random, then the hash function will perform well. However, if the number of buckets was 10 and we added the elements 20,30,40,50,60,70, then they would all end up in the same bucket and performance degenerates to a linked list. A good hash function can prevent this from occurring.
public int getHash(int x, int hashSize) {
// Use modulus as hash function.
return x % hashSize;
}
Resize
A hash set must be able to resize. When the ratio of number of elements to number of buckets, the chance of collision will increase more and more. So we must able to resize the number of buckets to support the number of elements to lower the chance of collision.
To resize efficiently, we can create two times the number of buckets and set them to empty and then insert all the elements in the old buckets to the new buckets.
public void resize() {
// Double number of buckets.
int newBucketsSize = bucketsSize * 2;
LinkedList<Integer>[] newBuckets = new LinkedList[newBucketsSize];
// Create new buckets.
for (int i = 0; i < newBucketsSize; i++) {
newBuckets[i] = new LinkedList<Integer>();
}
// Copy elements over and use new hashes.
for (int i = 0; i < bucketsSize; i++) {
for (Integer y : buckets[i]) {
int hash = getHash(y, newBucketsSize);
newBuckets[hash].push(y);
}
}
// Set new buckets.
buckets = newBuckets;
bucketsSize = newBucketsSize;
}
Insert
To insert an element in a hash set, we get the hash code from our hashing algorithm and insert the element into the corresponding bucket.
For example, if we want to insert 88 in the following hash set:

We compute the hash of 88 which is 8, and we insert it to the end of the bucket with hash 8.
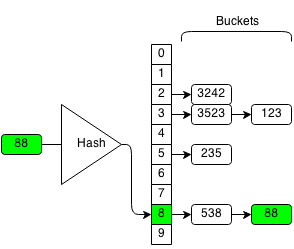
The function will return whether or not the operation was successful. If the bucket already contains the element, the operation will stop because we do not want to add duplicate elements into the set. If the bucket does not contain the element, we will insert it into the bucket and the operation is successful.
public boolean insert(int x) {
// Get hash of x.
int hash = getHash(x, bucketsSize);
// Get current bucket from hash.
LinkedList<Integer> curBucket = buckets[hash];
// Stop, if current bucket already has x.
if (curBucket.contains(x)) {
return false;
}
// Otherwise, add x to the bucket.
curBucket.push(x);
// Resize if the collision chance is higher than threshold.
if ((float) size / bucketsSize > COLLISION_CHANCE) {
resize();
}
size++;
return true;
}
Contains
To check if a hash set contains an element, we get the hash code from our hashing algorithm and check if the corresponding bucket contains the element.
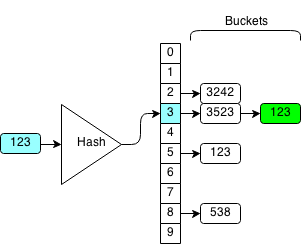
For example, if want to check if 123 is in the hash set:
We compute the hash of 123 which is 3 and search the bucket with hash 3.
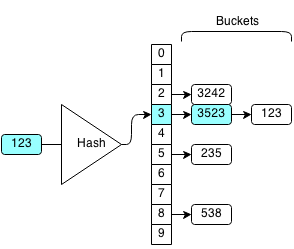
We iterate through the bucket until we find the element we want and return true. Otherwise, if we cannot find the element in the bucket we return false.
public boolean contains(int x) {
// Get hash of x.
int hash = getHash(x, bucketsSize);
// Get current bucket from hash.
LinkedList<Integer> curBucket = buckets[hash];
// Return if bucket contains x.
return curBucket.contains(x);
}
Remove
To remove an element from a hash set, we get the hash code from our hashing algorithm and remove the element from the corresponding bucket.
The function will return whether or not the operation was successful. If the bucket contains the element we can remove it from the linked list and the operation is successful. If the element is not in the bucket then the operation fails because we cannot remove something that is not there.
For example, we want to remove 123 from the hash set:
We compute the hash of 123 which is 3 and we search the bucket with hash 3.
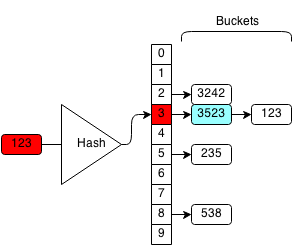
We iterate through each element in the bucket until we find 123.
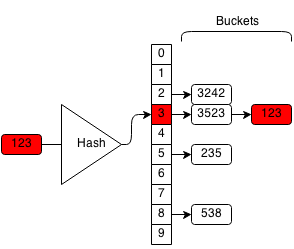
If we find the element, we delete the element from the bucket.
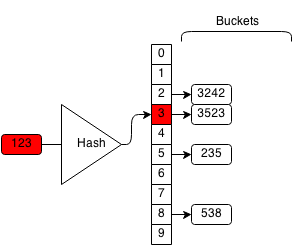
public boolean remove(int x) {
// Get hash of x.
int hash = getHash(x, bucketsSize);
// Get bucket from hash.
LinkedList<Integer> curBucket = buckets[hash];
// Remove x from bucket and return if operation successful.
return curBucket.remove((Integer) x);
}
Exercises
- Devise a hashing algorithm for strings.
- Calculate the probability of a collision occurring given the number of buckets and number of elements in the hash set.
- Prove that the runtime of all the operations are O(1).