Kruskal

Introduction

Prerequisites: Sorting, Minimum Spanning Tree

Kruskal's algorithm finds the minimum spanning tree using connected components.

If Kruskal's algorithm is implemented efficiently using a priority queue, the runtime is O(n log n).

Implementation

1. Uniquely label each node.
2. Take the edge with the minimum weight.
3. If the edge connects nodes A and B with different labels, all nodes with label B will be labeled with A. Otherwise, throw the edge away.
4. Repeat 2-3 until all the nodes have the same label.

Example

We first start with each node uniquely labelled as a letter.

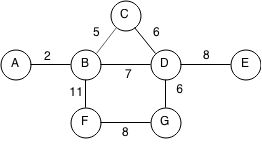
We first start with the edge with the smallest weight of 2 which was between A and B. We add B to A's component by labelling B as A.

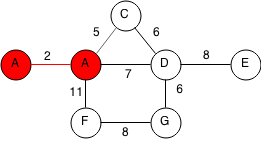
The next edge with the smallest weight is 5 which connects to C. We add C to A's component by labelling it as A.

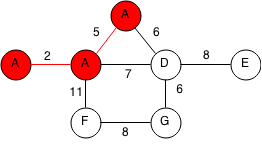
There is a tie between edges with the smallest weight of 6 and it doesn't matter which one we take. For the purpose of this example we will take the edge between D and G. We add G to D's component be labelling it as D.

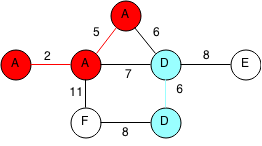
Next we take the other edge with weight 6. We are connecting the D and A components, thus we can label all the nodes with D as A.

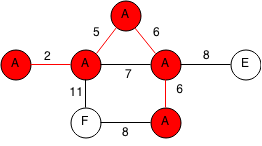
The next edge with smallest weight is 7 but it does not connect two different components, thus we discard the edge. The next two edges have weights 8 and we can randomly pick the edge to E. We add E to A's component by labelling it as A.

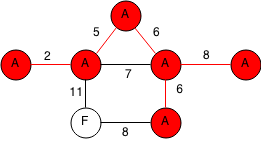
We take the other edge with weight 8 to F and add F to A's component by relabelling it as A.

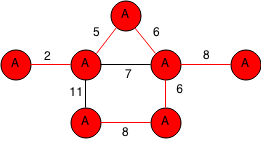
All the nodes are the same label and all part of the same component, thus by the algorithm, we have our minimum spanning tree.

Code

We can implement Kruskal's algorithm efficiently by using connected components.

class edge implements Comparable<edge> {
    int weight,source,dest;
    public edge(int source,int dest,int weight) {
        this.source = source;
        this.dest = dest;
        this.weight = weight;
    }
    public int compareTo(edge e) {
        return weight-e.weight;
    }
}
public static int getParent(int parents[], int x) {
  // Base Case: parent of x is itself.
  if (parents[x] == x) {
    return x;
  }
  // Set current's parent to highest parent.
  parents[x] = getParent(parents, parents[x]);

  // Returns parent.
  return parents[x];
}

public static int Kruskal(Vector<Vector<edge>> adjList) {
  int n = adjList.size();
  // Array of parents of each node. Nodes with the same parent are in the same component.
  int parents[] = new int[n];

  // Set parents of each node to itself.
  for (int i = 0; i < n; i++) {
    parents[i] = i;
  }

  int sum = 0;
  PriorityQueue<edge> edges = new PriorityQueue<edge>();

  // Iterate through each node.
  for (int i = 0; i < n; i++) {
    // Iterate through edges of node.
    for (int j = 0; j < adjList.get(i).size(); j++) {
      // Add edge to priority queue.
      edges.add(adjList.get(i).get(j));
    }
  }

  // Iterate through all edges.
  while (!edges.isEmpty()) {
    // Get edge with smallest weight.
    edge e = edges.poll();
    // Take edge if highest parent of source and destination nodes are
    // different i.e. take the edge if it connects different components
    if (getParent(parents, e.source) != getParent(parents, e.dest)) {
      // Set parent of source to highest parent of destination node.
      parents[e.source] = getParent(parents, e.dest);
      
      // Add edge weight to MST weight.
      sum += e.weight;
    }
  }

  // Return MST weight.
  return sum;
}

Exercises

1. Prove Kruskal's Algorithm works.
2. Extend Kruskals's to output the full minimum spanning tree used.