Introduction
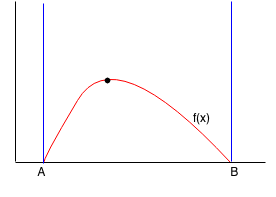
Ternary search is a search that finds a local minimum or maximum value in a function given an interval from A to B.
If there are multiple local minimum and maximum values, ternary search will only find one of them but it will not necessarily be the maximum or minimum.
Implementation
Suppose we have a function f(x) with only one max point between A and B. We want to find the point (M, f(M)) where f(M) is the maximum between A and B.
We split the range from A to B into three intervals. At every iteration of our algorithm, we can narrow down the range by 1/3 and we have a new interval. At every step, we can remove one of the intervals based on the following:
Let m1 by 1/3 of the way from A and B and let m2 be 2/3 of the way from B.

Case 1 : f(m1) < f(m2)
Case 1.1: m1 < m2 < M, so m1 < M
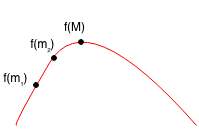
Case 1.2: m1 < M < m2, so m1 < M
Case 1.3: M < m1 < m2 is not possible.
Thus if f(m1) < f(m2), then m1 < M, so we only need to search from m1 to B.
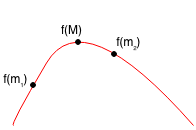
Case 2: f(m1) >= f(m2)
Case 2.1: m1 < M < m2, so M < m2
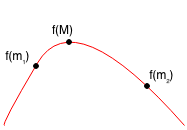
Case 2.2: M < m1 < m2, so M < m2
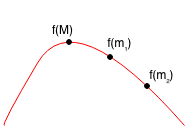
Case 2.3: m1 < m2 < M is not possible
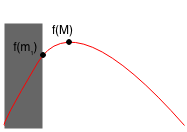
Thus, if f(m1) >= f(m2), then M < m2, so we only need to search from A to m2.
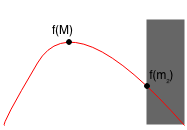
Therefore, based on the values of f(m1) and f(m2), we can always remove a third of the range. We can keep repeating this until the range is within a very small threshold such as 0.0001.
Example
Example of ternary search:
Suppose we have a function f(x) with a maximum point between A and B.

We find m1 (1/3) point and m2 (2/3) point between A and B.
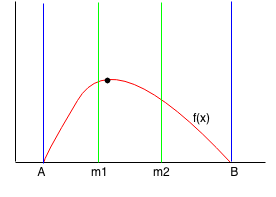
Since f(m1) > f(m2), then we can reduce the range from A to m2. We find the new m1 and m2 points.
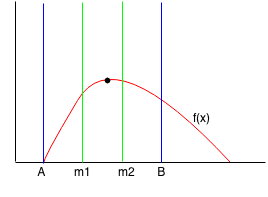
Since f(m1) < f(m2), then we can reduce the range from m1 to B. We find the new m1 and m2 points.
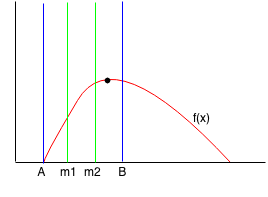
Since f(m1) < f(m2), then we can reduce the range from m1 to B. We find the new m1 and m2 points.
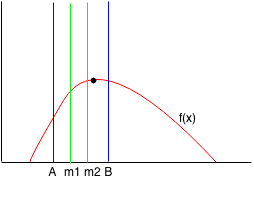
Since f(m1) < f(m2), then we can reduce the range from m1 to B. We find the new m1 and m2 points.
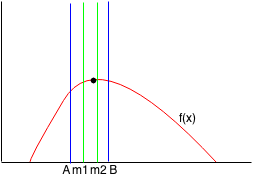
We keep repeating this until we narrow down the range to within a small threshold and we can find the point where f(x) is maximum.
Formalization
Let f(x) be the function. Let (a, b) be interval of search. Let tern(a,b) return M where f(M) is the maximum. Let m1 = a + (b - a) / 3 Let m2 = a + (b - a) * 2 / 3 tern(a,b) = (a + b) / 2 if |f(a) - f(b)| < epsilon tern(a,b) = tern(m1, b) if f(a) < f(b) tern(a,b) = tern(a, m2) otherwise
Code
public double tern(double a,double b){
if (Math.abs(f(a) - f(b)) < 0.0001) {
return (a + b) / 2.0;
}
double m1 = a + (b - a) / 3.0;
double m2 = a + (b - a) * 2.0 / 3.0;
if (f(m1) < f(m2)) {
return tern(m1, b);
} else {
return tern(a, m2);
}
}